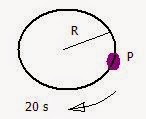
Equilibrio Rotacional

Equilibrio Rotacional

Es aquel equilibrio que ocurre cuando un cuerpo sufre un movimiento de rotacion o giro, al igual que el equilibrio traslacional debe tambien equilibrarse; surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
su fuerza se mide en torques o torcas es una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza.Explicado de una forma mas sencilla el torque es el producto entre la fuerza aplicada y la distancia a la cual se la aplica medida, generalmente, desde el punto que permanece fijo.
Así como una fuerza provoca una traslación, un torque produce una rotación.
El torque mide, de alguna manera, el estado de rotación que provoca la fuerza o la tendencia a producir una rotación.Del mismo modo que puede evitarse el desplazamiento de un objeto aplicando una fuerza contraria a la que lo hace mover, puede evitarse una rotación aplicando un torque contrario al que lo hace girar.

EQUILIBRIO TRASLACIONAL

Decimos que un objeto esta en equilibrio traslacional cuando se encuentra en reposo o bien se mueve en línea recta con velocidad constante.

Condiciones de equilibrio: Para que un cuerpo se encuentre en equilibrio, se requiere que la sumatoria de todas las fuerzas o torcas que actúan sobre él sea igual a cero. Se dice que todo cuerpo tiene dos tipos de equilibrio, el de traslación y el de rotación.

Traslación: Es aquel que surge en el momento en que todas las fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de las mismas sea igual a cero.

EFx = 0

EFy = 0

Aplicaciones: Se utiliza en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.

Problema del equilibrio traslacional

Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.

Primero se visualiza el problema de la siguiente manera:


A continuación se elabora su diagrama de cuerpo libre.

Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.

F1x = - F1 cos 45°*

F1y = F1 sen 45°

F2x = F2 cos 0° = F2

F2y = F2sen0°=0

F3x = F3cos90°=0

F3y = - F3 sen 90° = - 8 N*

Porque los cuadrantes en los que se localizan son negativos.

Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:

EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0

Por lo tanto tenemos lo siguiente:

EFx=-F1 cos 45+F2=0

F2=F1(0.7071)

EFy=-F1sen45-8N=0

8N=F1(0.7071)

F1=8N/0.7071=11.31 N

Para calcular F2, se sustituye F1 de la ecuación siguiente:

F2=F1(0.7071)

F2=11.31(0.7071)=8N

¡LEYES DE NEWTON!

Las leyes de Newton, también conocidas como leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular, aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.



Primera ley de Newton: Un cuerpo permanecerá en movimiento a la misma velocidad y dirección eternamente hasta que una fuerza externa lo haga cambiar de dirección, velocidad o estado (quedarse quieto). Lo mismo con un cuerpo en reposo (no se mueve) hasta que una fuerza lo haga cambiar de ese estado. 

Segunda ley: Fuerza = Masa x aceleración. O sea, entre más aceleración se le aplique a un objeto, mayor será su fuerza. Si quieres que un objeto se mueva más rápido, entonces muévalo con más fuerza. 


Tercera Ley: A cada acción corresponde una reacción de la misma magnitud pero en sentido contrario.
 Entre más fuerte golpees a alguien, más te dolerá a ti... si le pegas a la pared con mucha fuerza, te dolerá más 
la mano.

El movimiento circular uniformemente acelerado (MCUA) se presenta cuando una partícula o cuerpo sólido describe una trayectoria circular aumentando o disminuyendo la velocidad de forma constante en cada unidad de tiempo. Es decir, la partícula se mueve con aceleración constante.

En el dibujo se observa un ejemplo en donde la velocidad aumenta linealmente en el tiempo. Suponiendo que el tiempo en llegar del punto P₁ a P₂ sea una unidad de tiempo, la partícula viaja con una aceleración tangencialuniforme v, incrementándose esa cantidad en cada unidad de tiempo.

Posición

El desplazamiento de la partícula es más rápido o más lento según avanza el tiempo.

FORMULAS

MOVIMIENTO CIRCULAR UNIFORME

Movimiento circular uniforme

En física, el movimiento circular uniforme (también denominado movimiento uniformemente circular) describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.

Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.

FORMULAS

EJERCICIO

Una partícula P viaja a velocidad constante en un círculo de 3 m de radio y completa una revolución en 20 s (véase la figura). a) encuentre el valor de la aceleración; b) la rapidez con la que viaja.

a) Los datos dados son el período T y la velocidad de la partícula, con ellos, se puede obtener la aceleración:

b) La rapidez se encuentra mediante la relación de la aceleración y el radio: