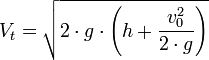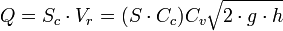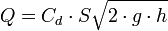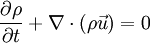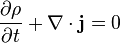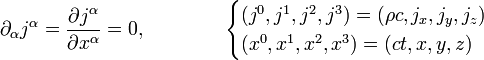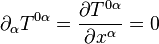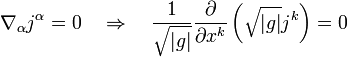PROCESOS TERMODINÁMICOS Y TRANSFERENCIA DE CALOR
La termodinámica se interesa en la cantidad de transferencia de calor a medida que un sistema pasa por un proceso, sin indicar cuánto tiempo transcurrirá. Un estudio termodinámico sencillamente nos dice cuánto calor debe transferirse para que se realice un cambio de estado específico, con el fin de cumplir con el principio de conservación de la energía. En la experiencia nos enfocamos más en la velocidad de la transferencia de calor que en la cantidad transferida. La termodinámica trata de los estados en equilibrio y de los cambios que ocurren entre un estado de equilibrio y otro. Por otra parte, la transferencia de calor se ocupa de los sistemas en los que se presenta desequilibrio térmico y, por tanto, existe una condición de no equilibrio. En consecuencia, el estudio de la transferencia de calor no puede basarse sólo en los principios de la termodinámica; sin embargo, existen leyes de la termodinámica que constituyen la base científica de la transferencia de calor.
La primera ley de la termodinámica establece que la velocidad de transferencia de energía hacia un sistema es igual a la velocidad de incremento de la energía de dicho sistema. Su segunda ley, establece que el calor se transfiere en dirección de la temperatura decreciente. El requisito básico para la transferencia de calor es la presencia de una diferencia de temperatura. No existe la más mínima posibilidad de que se dé transferencia neta de calor entre dos medios que están a la misma temperatura, esta diferencia de temperaturas constituye la condición básica necesaria para que se dé transferencia de calor.
Anteriormente mencionamos que el análisis termodinámico no se ocupa de la velocidad de la transferencia de calor en cierta dirección pero, ahora, podemos decir que este parámetro depende de la magnitud del gradiente de temperatura (o diferencia de temperatura por unidad de longitud, o la razón o relación de cambio de la temperatura en esa dirección). A mayor gradiente de temperatura, mayor es la velocidad de transferencia de calor.
Los problemas de capacidad nominal se ocupan de la determinación de la velocidad de transferencia de calor para un sistema existente con una diferencia específica de temperatura. Los problemas de dimensionamiento se ocupan de la determinación del tamaño de un sistema con el fin de transferir calor a una velocidad determinada para una diferencia específica de la temperatura. Un proceso o un equipo de transferencia de calor puede ser analizado de forma experimental o de forma analítica. El procedimiento experimental tiene la ventaja de tratar con el sistema físico real y, gracias a ello, la cantidad deseada se determina mediante medición, dentro de los límites del error experimental. El procedimiento analítico tiene la ventaja de que es rápido y barato, pero los resultados obtenidos dependen de la exactitud de las hipótesis e idealizaciones establecidas en el análisis. En los estudios de transferencia de calor a menudo se logra una buena aproximación reduciendo, mediante el análisis, las opciones a solo unas cuantas y, a continuación, verificando los hallazgos experimentalmente.
Por amor a la física
martes, 8 de diciembre de 2015
CAMBIO DE ESTADO
Es la evolución de la materia entre varios estados de agregación sin que ocurra un cambio en su composición. Los tres estados más estudiados y comunes en la Tierra son el sólido, el líquido y el gaseoso; no obstante, el estado de agregación más común en el Universo es el plasma, material del que están compuestas las estrellas (si se descarta la materia oscura).
Son los procesos en los que un estado de la materia cambia a otro manteniendo una semejanza en su composición. A continuación se describen los diferentes cambios de estado o transformaciones de fase de la materia:
Fusión: Es el paso de un sólido al estado líquido por medio del calor; durante este proceso endotérmico (proceso que absorbe energía para llevarse a cabo este cambio) hay un punto en que la temperatura permanece constante. El "punto de fusión" es la temperatura a la cual el sólido se funde, por lo que su valor es particular para cada sustancia. Dichas moléculas se moverán en una forma independiente, transformándose en un líquido. Un ejemplo podría ser un hielo derritiéndose, pues pasa de estado sólido al líquido.
Solidificación: Es el paso de un líquido a sólido por medio del enfriamiento; el proceso es exotérmico. El "punto de solidificación" o de congelación es la temperatura a la cual el líquido se solidifica y permanece constante durante el cambio, y coincide con el punto de fusión si se realiza de forma lenta (reversible); su valor es también específico.
Vaporización y ebullición: Son los procesos físicos en los que un líquido pasa a estado gaseoso. Si se realiza cuando la temperatura de la totalidad del líquido iguala al punto de ebullición del líquido a esa presión continuar calentándose el líquido, éste absorbe el calor, pero sin aumentar la temperatura: el calor se emplea en la conversión del agua en estado líquido en agua en estado gaseoso, hasta que la totalidad de la masa pasa al estado gaseoso. En ese momento es posible aumentar latemperatura del gas.
Condensación: Se denomina condensación al cambio de estado de la materia que se pasa de forma gaseosa a forma líquida. Es el proceso inverso a la vaporización. Si se produce un paso de estado gaseoso a estado sólido de manera directa, el proceso es llamado sublimación inversa. Si se produce un paso del estado líquido a sólido se denomina solidificación.
Sublimación: Es el proceso que consiste en el cambio de estado de la materia sólida al estado gaseoso sin pasar por el estado líquido. Al proceso inverso se le denomina Sublimación inversa; es decir, el paso directo del estado gaseoso al estado sólido. Un ejemplo clásico de sustancia capaz de sublimarse es el hielo seco.
Desionización: Es el cambio de un plasma a gas.
Ionización: Es el cambio de un gas a un plasma.
Es importante hacer notar que en todas las transformaciones de fase de las sustancias, éstas no se transforman en otras sustancias, solo cambia su estado físico.
Las diferentes transformaciones de fase de la materia en este caso las del agua son necesarias y provechosas para la vida y el sustento del hombre cuando se desarrollan normalmente.
Los cambios de estado están divididos generalmente en dos tipos: progresivos y regresivos.
Cambios progresivos: Vaporización, fusión y sublimación progresiva.
Cambios regresivos: Condensación, solidificación y sublimación regresiva
EQUILIBRIO TÉRMICO
El equilibrio térmico es aquel estado en el cual se igualan las temperaturas de dos cuerpos, las cuales, en sus condiciones iniciales presentaban diferentes temperaturas. Una vez que las temperaturas se equiparan se suspende el flujo de calor, llegando ambos cuerpos al mencionado equilibrio térmico.
Una vez que las temperaturas se equiparan se suspende el flujo de calor, llegando ambos cuerpos al mencionado equilibrio término.
El de equilibrio térmico es un concepto que forma parte de la termodinámica, la rama de la física que se ocupa de describir los estados de equilibrio a un nivel macroscópico.
En física, el nivel macroscópico es el nivel de descripción en que la posición o estado físico concreto de las partículas que integran un cuerpo puede ser resumido en una ecuación de estado que sólo incluye magnitudes extensivas (volumen, longitud, masa) y magnitudes intensivas promedio (presión, temperatura).
El concepto de equilibrio térmico es la base de la llamada Ley Cero de la Termodinámica. Esta ley proposición fue enunciada por R. H. Fowler en 1931. La ley cero de la termodinámica se enuncia diciendo:
La experiencia indica que si dos sistemas A y B se encuentran, cada uno por separado, en equilibrio térmico con un tercer sistema, que llamaremos C, entonces A y B se encuentran en equilibrio térmico entre sí.
Cuando dos sistemas se encuentran en contacto mecánico directo, o en su defecto, separados mediante una superficie que facilita la transferencia de calor, superficie diatérmica, se dirá que ambos están en contacto térmico. Mientras tanto, al cabo de un tiempo, aunque los dos sistemas que se hallan en contacto térmico se encuentren dispuestos de tal manera que no puedan mezclarse o aunque estén colocados en el interior de un espacio en el cual es imposible que intercambien calor con el exterior, indefectiblemente, alcanzarán el estado de equilibrio térmico.
Para poder conocer la temperatura que presenta un cuerpo o sustancia se emplea el dispositivo del termómetro. Cuando el termómetro entra en contacto térmico con el cuerpo en cuestión ambos alcanzarán el equilibrio térmico y entonces al encontrase en la misma temperatura, sabremos que la temperatura que nos indicará el termómetro en su índice será la temperatura del cuerpo que nos ocupa.
Es la evolución de la materia entre varios estados de agregación sin que ocurra un cambio en su composición. Los tres estados más estudiados y comunes en la Tierra son el sólido, el líquido y el gaseoso; no obstante, el estado de agregación más común en el Universo es el plasma, material del que están compuestas las estrellas (si se descarta la materia oscura).
Son los procesos en los que un estado de la materia cambia a otro manteniendo una semejanza en su composición. A continuación se describen los diferentes cambios de estado o transformaciones de fase de la materia:
Fusión: Es el paso de un sólido al estado líquido por medio del calor; durante este proceso endotérmico (proceso que absorbe energía para llevarse a cabo este cambio) hay un punto en que la temperatura permanece constante. El "punto de fusión" es la temperatura a la cual el sólido se funde, por lo que su valor es particular para cada sustancia. Dichas moléculas se moverán en una forma independiente, transformándose en un líquido. Un ejemplo podría ser un hielo derritiéndose, pues pasa de estado sólido al líquido.
Solidificación: Es el paso de un líquido a sólido por medio del enfriamiento; el proceso es exotérmico. El "punto de solidificación" o de congelación es la temperatura a la cual el líquido se solidifica y permanece constante durante el cambio, y coincide con el punto de fusión si se realiza de forma lenta (reversible); su valor es también específico.
Vaporización y ebullición: Son los procesos físicos en los que un líquido pasa a estado gaseoso. Si se realiza cuando la temperatura de la totalidad del líquido iguala al punto de ebullición del líquido a esa presión continuar calentándose el líquido, éste absorbe el calor, pero sin aumentar la temperatura: el calor se emplea en la conversión del agua en estado líquido en agua en estado gaseoso, hasta que la totalidad de la masa pasa al estado gaseoso. En ese momento es posible aumentar latemperatura del gas.
Condensación: Se denomina condensación al cambio de estado de la materia que se pasa de forma gaseosa a forma líquida. Es el proceso inverso a la vaporización. Si se produce un paso de estado gaseoso a estado sólido de manera directa, el proceso es llamado sublimación inversa. Si se produce un paso del estado líquido a sólido se denomina solidificación.
Sublimación: Es el proceso que consiste en el cambio de estado de la materia sólida al estado gaseoso sin pasar por el estado líquido. Al proceso inverso se le denomina Sublimación inversa; es decir, el paso directo del estado gaseoso al estado sólido. Un ejemplo clásico de sustancia capaz de sublimarse es el hielo seco.
Desionización: Es el cambio de un plasma a gas.
Ionización: Es el cambio de un gas a un plasma.
Es importante hacer notar que en todas las transformaciones de fase de las sustancias, éstas no se transforman en otras sustancias, solo cambia su estado físico.
Las diferentes transformaciones de fase de la materia en este caso las del agua son necesarias y provechosas para la vida y el sustento del hombre cuando se desarrollan normalmente.
Los cambios de estado están divididos generalmente en dos tipos: progresivos y regresivos.
Cambios progresivos: Vaporización, fusión y sublimación progresiva.
Cambios regresivos: Condensación, solidificación y sublimación regresiva
EQUILIBRIO TÉRMICO
El equilibrio térmico es aquel estado en el cual se igualan las temperaturas de dos cuerpos, las cuales, en sus condiciones iniciales presentaban diferentes temperaturas. Una vez que las temperaturas se equiparan se suspende el flujo de calor, llegando ambos cuerpos al mencionado equilibrio térmico.
Una vez que las temperaturas se equiparan se suspende el flujo de calor, llegando ambos cuerpos al mencionado equilibrio término.
El de equilibrio térmico es un concepto que forma parte de la termodinámica, la rama de la física que se ocupa de describir los estados de equilibrio a un nivel macroscópico.
En física, el nivel macroscópico es el nivel de descripción en que la posición o estado físico concreto de las partículas que integran un cuerpo puede ser resumido en una ecuación de estado que sólo incluye magnitudes extensivas (volumen, longitud, masa) y magnitudes intensivas promedio (presión, temperatura).
El concepto de equilibrio térmico es la base de la llamada Ley Cero de la Termodinámica. Esta ley proposición fue enunciada por R. H. Fowler en 1931. La ley cero de la termodinámica se enuncia diciendo:
La experiencia indica que si dos sistemas A y B se encuentran, cada uno por separado, en equilibrio térmico con un tercer sistema, que llamaremos C, entonces A y B se encuentran en equilibrio térmico entre sí.
Cuando dos sistemas se encuentran en contacto mecánico directo, o en su defecto, separados mediante una superficie que facilita la transferencia de calor, superficie diatérmica, se dirá que ambos están en contacto térmico. Mientras tanto, al cabo de un tiempo, aunque los dos sistemas que se hallan en contacto térmico se encuentren dispuestos de tal manera que no puedan mezclarse o aunque estén colocados en el interior de un espacio en el cual es imposible que intercambien calor con el exterior, indefectiblemente, alcanzarán el estado de equilibrio térmico.
Para poder conocer la temperatura que presenta un cuerpo o sustancia se emplea el dispositivo del termómetro. Cuando el termómetro entra en contacto térmico con el cuerpo en cuestión ambos alcanzarán el equilibrio térmico y entonces al encontrase en la misma temperatura, sabremos que la temperatura que nos indicará el termómetro en su índice será la temperatura del cuerpo que nos ocupa.
ENERGÍA INTERNA
En física, la energía interna (U) de un sistema intenta ser un reflejo de la energía a escala macroscópica. Más concretamente, es la suma de:
la energía cinética interna, es decir, de las sumas de las energías cinéticas de las individualidades que lo forman respecto al centro de masas del sistema,
la energía potencial interna, que es la energía potencial asociada a las interacciones entre estas individualidades.1
La energía interna no incluye la energía cinética traslacional o rotacional del sistema como un todo. Tampoco incluye la energía potencial que el cuerpo pueda tener por su localización en un campo gravitacional o electrostático externo.
Todo cuerpo posee una energía acumulada en su interior equivalente a la energía cinética interna más la energía potencial interna.
Si pensamos en constituyentes atómicos o moleculares, será el resultado de la suma de la energía cinética de las moléculas oátomos que constituyen el sistema (de sus energías de traslación, rotación y vibración) y de la energía potencial intermolecular (debida a las fuerzas intermoleculares) e intramolecular de la energía de enlace.
En un gas ideal monoatómico bastará con considerar la energía cinética de traslación de sus átomos.
En un gas ideal poliatómico, deberemos considerar además la energía vibracional y rotacional de las mismas.
En un líquido o sólido deberemos añadir la energía potencial que representa las interacciones moleculares.
Desde el punto de vista de la termodinámica, en un sistema cerrado (o sea, de paredes impermeables), la variación total de energía interna es igual a la suma de las cantidades de energía comunicadas al sistema en forma de calor y de trabajo \Delta U = Q - W(En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo dU es una diferencial exacta, a diferencia de \eth Q, que depende del proceso.
MÁQUINAS TERMODINÁMICAS
Una máquina térmica es un conjunto de elementos mecánicos que permite intercambiar energía, generalmente a través de un eje, mediante la variación de energía de un fluido que varía su densidad significativamente al atravesar la máquina. Se trata de una máquina de fluido en la que varía el volumen específico del fluido en tal magnitud que los efectos mecánicos y los efectos térmicos son interdependientes.
Por el contrario, en una máquina hidráulica, que es otro tipo de máquina de fluido, la variación de densidad es suficientemente pequeña como para poder desacoplar el análisis de los efectos mecánicos y el análisis de los efectos térmicos, llegando a despreciar los efectos térmicos en gran parte de los casos. Tal es el caso de una bomba hidráulica, a través de la cual pasa líquido. Alejándose de lo que indica la etimología de la palabra «hidráulica», también puede considerarse como máquina hidráulica un ventilador, pues, aunque el aire es un fluido compresible, la variación de volumen específico no es muy significativa con el propósito de que no se desprenda la capa límite.
En una máquina térmica, la compresibilidad del fluido no es despreciable y es necesario considerar su influencia en la transformación de energía.
En un principio se podría definir a una máquina térmica como un dispositivo, equipo o una instalación destinada a la producción de trabajo en virtud de un aporte calórico. Aunque en algunas definiciones se identifican como sinónimos los términos «máquina térmica motora» y «motor térmico», en otras se diferencian ambos conceptos. Al diferenciarlos, se considera que un motor térmico es un conjunto de elementos mecánicos que permite obtener energía mecánica a partir de la energía térmica obtenida mediante una reacción de combustión o una reacción nuclear. Un motor térmico dispone de lo necesario para obtener energía térmica, mientras que una máquina térmica motora necesita energía térmica para funcionar, mediante un fluido que dispone de más energía a la entrada que a la salida.
Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:
Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose energía mecánica en el eje.
Máquinas térmicas generadoras, en las cuales la energía del fluido aumenta al atravesar la máquina, precisándose energía mecánica en el eje.
En física, la energía interna (U) de un sistema intenta ser un reflejo de la energía a escala macroscópica. Más concretamente, es la suma de:
la energía cinética interna, es decir, de las sumas de las energías cinéticas de las individualidades que lo forman respecto al centro de masas del sistema,
la energía potencial interna, que es la energía potencial asociada a las interacciones entre estas individualidades.1
La energía interna no incluye la energía cinética traslacional o rotacional del sistema como un todo. Tampoco incluye la energía potencial que el cuerpo pueda tener por su localización en un campo gravitacional o electrostático externo.
Todo cuerpo posee una energía acumulada en su interior equivalente a la energía cinética interna más la energía potencial interna.
Si pensamos en constituyentes atómicos o moleculares, será el resultado de la suma de la energía cinética de las moléculas oátomos que constituyen el sistema (de sus energías de traslación, rotación y vibración) y de la energía potencial intermolecular (debida a las fuerzas intermoleculares) e intramolecular de la energía de enlace.
En un gas ideal monoatómico bastará con considerar la energía cinética de traslación de sus átomos.
En un gas ideal poliatómico, deberemos considerar además la energía vibracional y rotacional de las mismas.
En un líquido o sólido deberemos añadir la energía potencial que representa las interacciones moleculares.
Desde el punto de vista de la termodinámica, en un sistema cerrado (o sea, de paredes impermeables), la variación total de energía interna es igual a la suma de las cantidades de energía comunicadas al sistema en forma de calor y de trabajo \Delta U = Q - W(En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo dU es una diferencial exacta, a diferencia de \eth Q, que depende del proceso.
MÁQUINAS TERMODINÁMICAS
Una máquina térmica es un conjunto de elementos mecánicos que permite intercambiar energía, generalmente a través de un eje, mediante la variación de energía de un fluido que varía su densidad significativamente al atravesar la máquina. Se trata de una máquina de fluido en la que varía el volumen específico del fluido en tal magnitud que los efectos mecánicos y los efectos térmicos son interdependientes.
Por el contrario, en una máquina hidráulica, que es otro tipo de máquina de fluido, la variación de densidad es suficientemente pequeña como para poder desacoplar el análisis de los efectos mecánicos y el análisis de los efectos térmicos, llegando a despreciar los efectos térmicos en gran parte de los casos. Tal es el caso de una bomba hidráulica, a través de la cual pasa líquido. Alejándose de lo que indica la etimología de la palabra «hidráulica», también puede considerarse como máquina hidráulica un ventilador, pues, aunque el aire es un fluido compresible, la variación de volumen específico no es muy significativa con el propósito de que no se desprenda la capa límite.
En una máquina térmica, la compresibilidad del fluido no es despreciable y es necesario considerar su influencia en la transformación de energía.
En un principio se podría definir a una máquina térmica como un dispositivo, equipo o una instalación destinada a la producción de trabajo en virtud de un aporte calórico. Aunque en algunas definiciones se identifican como sinónimos los términos «máquina térmica motora» y «motor térmico», en otras se diferencian ambos conceptos. Al diferenciarlos, se considera que un motor térmico es un conjunto de elementos mecánicos que permite obtener energía mecánica a partir de la energía térmica obtenida mediante una reacción de combustión o una reacción nuclear. Un motor térmico dispone de lo necesario para obtener energía térmica, mientras que una máquina térmica motora necesita energía térmica para funcionar, mediante un fluido que dispone de más energía a la entrada que a la salida.
Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:
Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose energía mecánica en el eje.
Máquinas térmicas generadoras, en las cuales la energía del fluido aumenta al atravesar la máquina, precisándose energía mecánica en el eje.
martes, 3 de noviembre de 2015
Teorema de bernoulli
TEOREMA DE DANIEL BERNOULLI
El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido en reposo moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:
Cinética: es la energía debida a la velocidad que posea el fluido.
Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.
La siguiente ecuación conocida como “Ecuación de Bernoulli” (Trinomio de Bernoulli) consta de estos mismos términos.
donde:
 = velocidad del fluido en la sección considerada.
= velocidad del fluido en la sección considerada. = densidad del fluido.
= densidad del fluido. = presión a lo largo de la línea de corriente.
= presión a lo largo de la línea de corriente. = aceleración gravitatoria
= aceleración gravitatoria = altura en la dirección de la gravedad desde una cota de referencia.
= altura en la dirección de la gravedad desde una cota de referencia.
Para aplicar la ecuación se deben realizar los siguientes supuestos:
Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.
Caudal constante
Flujo incompresible, donde ρ es constante.
La ecuación se aplica a lo largo de una línea de corriente o en un flujo rotacional
Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.
Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.
Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término  se suele agrupar con
se suele agrupar con  (donde
(donde  ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia
) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia
También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por  , de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
Teorema de torricelli
El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeñoorificio, bajo la acción de la gravedad.
La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio.
Matemáticamente:
donde:
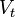 es la velocidad teórica del líquido a la salida del orificio
es la velocidad teórica del líquido a la salida del orificio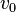 es la velocidad de aproximación o inicial.
es la velocidad de aproximación o inicial.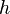 es la distancia desde la superficie del líquido al centro del orificio.
es la distancia desde la superficie del líquido al centro del orificio.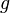 es la aceleración de la gravedad
es la aceleración de la gravedad
Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:
donde:
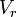 es la velocidad real media del líquido a la salida del orificio
es la velocidad real media del líquido a la salida del orificio es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
tomando  =1
=1
 =1
=1
Experimentalmente se ha comprobado que la velocidad media de un chorro de un orificio de pared delgada, es un poco menor que la ideal, debido a la viscosidad del fluido y otros factores tales como la tensión superficial, de ahí el significado de este coeficiente de velocidad.
CAUDAL DESCARGADO[EDITAR]
El caudal o volumen del fluido que pasa por el orificio en un tiempo, 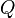 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 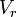 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
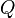 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 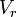 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
en donde
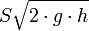 representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.
representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.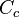 es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída
es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída  y la del orificio
y la del orificio 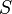 . Suele estar en torno a 0,65.
. Suele estar en torno a 0,65.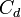 es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes.
es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes. 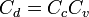
ecuación de continuidad
En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial.
TEORÍA ELECTROMAGNÉTICA[EDITAR]
En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de la densidad de carga respecto del tiempo:
En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.
Esta ecuación establece la conservación de la carga.
MECÁNICA DE FLUIDOS[EDITAR]
En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:
donde  es la densidad, t el tiempo y
es la densidad, t el tiempo y 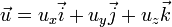 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.
 es la densidad, t el tiempo y
es la densidad, t el tiempo y 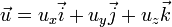 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.MECÁNICA CUÁNTICA[EDITAR]
En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:1
Donde  es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 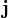 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
 es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 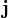 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:MECÁNICA RELATIVISTA[EDITAR]
En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como:
La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
Donde 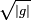 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
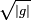 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
La conservación de la masa de fluido a través de dos secciones (sean éstas A1 y A2) de un conducto (tubería) o tubo de corriente establece que: la masa que entra es igual a la masa que sale.
Definición de tubo de corriente: superficie formada por las líneas de corriente.
Corolario 2: solo hay flujo de corriente si V es diferente de 0.
La ecuación de continuidad se puede expresar como:
Cuando  , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
 , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
o de otra forma:
 (el caudal que entra es igual al que sale)
(el caudal que entra es igual al que sale)
Donde:
- Q = caudal (metro cúbico por segundo;
 )
) - V = velocidad

- A = area transversal del tubo de corriente o conducto

Que se cumple cuando entre dos secciones de la conducción no se acumula masa, es decir, siempre que el fluido sea incompresible y por lo tanto su densidad sea constante. Esta condición la satisfacen todos los líquidos y, particularmente, el agua.
En general la geometría del conducto es conocida, por lo que el problema se reduce a estimar la velocidad media del fluido en una sección dada.
EL PRINCIPIO DE BERNOULLI
A estos efectos es de aplicación el Principio de Bernoulli, que no es sino la formulación, a lo largo de una línea de flujo, de la Ley de conservación de la energía. Para un fluido ideal, sin rozamiento, se expresa  , donde
, donde
 , donde
, donde- g aceleración de la gravedad
 densidad del fluido
densidad del fluido- P presión
Se aprecia que los tres sumandos son, dimensionalmente, una longitud (o altura), por lo que el Principio normalmente se expresa enunciando que, a lo largo de una línea de corriente la suma de la altura geométrica, la altura de velocidad y la altura de presión se mantiene constante.
Cuando el fluido es real, para circular entre dos secciones de la conducción deberá vencer las resistencias debidas al rozamiento con las paredes interiores de la tubería, así como las que puedan producirse al atravesar zonas especiales como válvulas, ensanchamientos, codos, etc. Para vencer estas resistencias deberá emplear o perder una cierta cantidad de energía o, con la terminología derivada del Principio de Bernoulli de altura, que ahora se puede formular, entre las secciones 1 y 2:
 , o lo que es igual
, o lo que es igual
Suscribirse a:
Comentarios (Atom)