En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial.
TEORÍA ELECTROMAGNÉTICA[EDITAR]
En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de la densidad de carga respecto del tiempo:
En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.
Esta ecuación establece la conservación de la carga.
MECÁNICA DE FLUIDOS[EDITAR]
En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:
donde  es la densidad, t el tiempo y
es la densidad, t el tiempo y 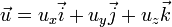 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.
 es la densidad, t el tiempo y
es la densidad, t el tiempo y 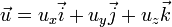 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.MECÁNICA CUÁNTICA[EDITAR]
En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:1
Donde  es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 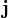 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
 es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 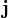 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:MECÁNICA RELATIVISTA[EDITAR]
En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como:
La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
Donde 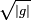 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
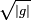 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
La conservación de la masa de fluido a través de dos secciones (sean éstas A1 y A2) de un conducto (tubería) o tubo de corriente establece que: la masa que entra es igual a la masa que sale.
Definición de tubo de corriente: superficie formada por las líneas de corriente.
Corolario 2: solo hay flujo de corriente si V es diferente de 0.
La ecuación de continuidad se puede expresar como:
Cuando  , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
 , que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
o de otra forma:
 (el caudal que entra es igual al que sale)
(el caudal que entra es igual al que sale)
Donde:
- Q = caudal (metro cúbico por segundo;
 )
) - V = velocidad

- A = area transversal del tubo de corriente o conducto

Que se cumple cuando entre dos secciones de la conducción no se acumula masa, es decir, siempre que el fluido sea incompresible y por lo tanto su densidad sea constante. Esta condición la satisfacen todos los líquidos y, particularmente, el agua.
En general la geometría del conducto es conocida, por lo que el problema se reduce a estimar la velocidad media del fluido en una sección dada.
EL PRINCIPIO DE BERNOULLI
A estos efectos es de aplicación el Principio de Bernoulli, que no es sino la formulación, a lo largo de una línea de flujo, de la Ley de conservación de la energía. Para un fluido ideal, sin rozamiento, se expresa  , donde
, donde
 , donde
, donde- g aceleración de la gravedad
 densidad del fluido
densidad del fluido- P presión
Se aprecia que los tres sumandos son, dimensionalmente, una longitud (o altura), por lo que el Principio normalmente se expresa enunciando que, a lo largo de una línea de corriente la suma de la altura geométrica, la altura de velocidad y la altura de presión se mantiene constante.
Cuando el fluido es real, para circular entre dos secciones de la conducción deberá vencer las resistencias debidas al rozamiento con las paredes interiores de la tubería, así como las que puedan producirse al atravesar zonas especiales como válvulas, ensanchamientos, codos, etc. Para vencer estas resistencias deberá emplear o perder una cierta cantidad de energía o, con la terminología derivada del Principio de Bernoulli de altura, que ahora se puede formular, entre las secciones 1 y 2:
 , o lo que es igual
, o lo que es igual

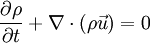
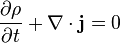

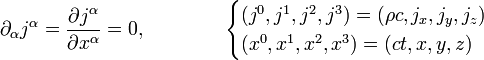
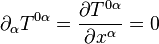
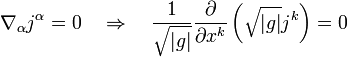
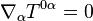

No hay comentarios.:
Publicar un comentario